Modéliser un mouvement de foule aléatoire [programmation]
Salut Itch !
Ce billet est là pour échanger sur la programmation de Meurtres en coups lisses (réalisé lors d'une JAM de 3 jours), en s'appuyant plus précisément sur la modélisation mathématiques de la marche aléatoire de la foule au sein d'un espace clos.
Comment et sur quoi je code ?
Bien que mes études m'ont fait découvrir le langage C++, un peu d'HTML et de CSS, je me suis principalement formé seul à la programmation, étant tombé dedans tout petit, vers mes 5 ans (sur le pénible langage Basic intégré à toutes les consoles Atari de l'époque). Mon principal atout : ma formation poussée en mathématiques, un outil formidable pour renforcer ses capacités d'abstraction et de modélisation.
J'ai toujours joué aux jeux vidéos (dès mes 2 ans à vrai dire), et dès que j'ai compris que je pouvais en programmer, c'est devenu mon objectif. Après quelques essais en C++, quand j'ai découvert l'existence de GameMaker, logiciel "gratuit", qui s'occupait à ma place de la gestion des pointeurs (à devenir fou quand on programme en simple amateur), je n'ai pas hésité. Depuis, je suis très familier avec cet outil (et je me forme sur Unreal5 actuellement).
Un prototype rapide
Nous avions vite trouvé cette idée d'une foule de personnage parmi lesquels les joueurs se cacheraient, nous savions qu'elle se déplacerait de manière aléatoire et chaotique, mais que des événements se produiraient pour compliquer la tâche des joueurs. Pour permettre à l'équipe de la JAM de se faire une idée immédiate des possibilités de déplacements de la foule (et de mes compétences), avant même la création du moindre asset graphique, j'ai rapidement proposé des prototypes :
Il s'agit ici du second prototype proposé à l'équipe, la foule se déplace aléatoirement, on peut lui ordonner de se synchroniser (pour l'événement chorégraphie), et les joueurs peuvent se déplacer et tuer les PNJ (ou s'entretuer). En l'absence d'assets, les animaux sont représentés par des points de couleur, plus gros lorsqu'il s'agit des joueurs. Un animal mort apparaît en blanc.
Un mouvement de foule aléatoire basique ?
Lors des phases de marche aléatoire, chaque animal de la foule altèrne entre moment d'immobilité, et moment de marche à une vitesse fixée aléatoirement, vers une direction fixée aléatoirement (en changeant de temps en temps de direction durant la marche, mais négligeons ce détail).
L'objet obj_animal dispose donc des variables suivantes :
- coordonnée x
- coordonnée y
- vitesse
- direction_aleatoire
Durant la marche, les deux lignes de code suivantes sont éxécutées :

Les fonctions cosinus et sinus servent ici à répartir la vitesse à la fois horizontalement en x, et verticalement en y. Elles garantissent que l'animal se déplacera exactement à la vitesse fixée, quelque soit la direction vers laquelle il marche.
De plus, pour éviter que les animaux ne quittent la scène, on s'assure que leurs coordonnées (x ; y) ne dépassent pas certaines valeurs, avec les lignes de codes suivantes :

Résultat...
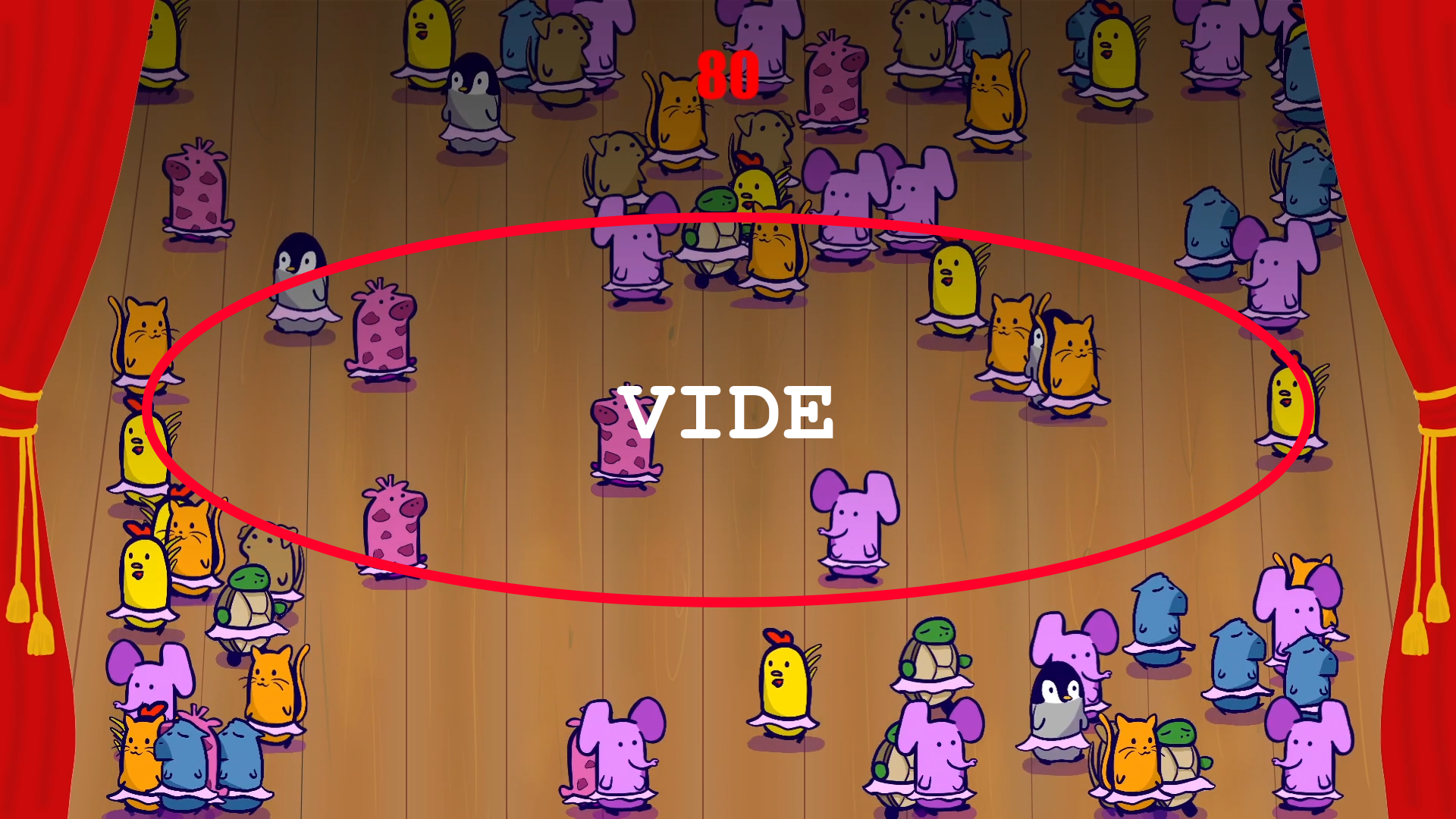
Eh oui. Les bêbêtes s'agglutinent sur les bords de l'écran. En effet, lorsqu'elles sont au centre, il est garanti qu'elles partiront vers un bord de l'écran. En revanche, lorsqu'elles sont au bord de l'écran, par exemple en bas, au moment de se remettre en marche, si la direction choisie aléatoirement ne va pas vers le haut (1 chance sur 2 donc), elles resteront alors sur le bord où elles se trouvent...
La solution adoptée
De cette première analyse, nous comprenons bien que nos créatures, lorsqu'elles se choisissent une nouvelle direction aléatoire de marche, doivent être poussées à repartir vers le centre (il va falloir orienter le hasard). Plus une créature est à gauche, plus elle doit vouloir aller à droite. Plus elle est à droite, plus elle doit vouloir aller à gauche (de même pour haut et bas). Ces "attracteurs" doivent être d'autant plus forts qu'une créature est loin du centre (sinon nous inverserions simplement le problème, toutes les créatures s'agglutineraient au centre de la pièce, et délaisseraient les bords de la scène). Voilà à quoi cela va ressembler.

Alors, alors, alors... Qu'est-ce qu'il s'est passé ? La vitesse est dorénavant multipliée par une expression plus complexe. Prenons la ligne des x.
cos(direction_aleatoire) multiplie toujours vitesse, comme dans l'exemple précédent. Mais nous lui ajoutons avant cela distance_bord_GD*cos(dir_GD). Si distance_bord_GD était nulle, nous retrouverions notre formule précédente. Or, voici les lignes de code qui calculent la valeur de distance_bord_GD :
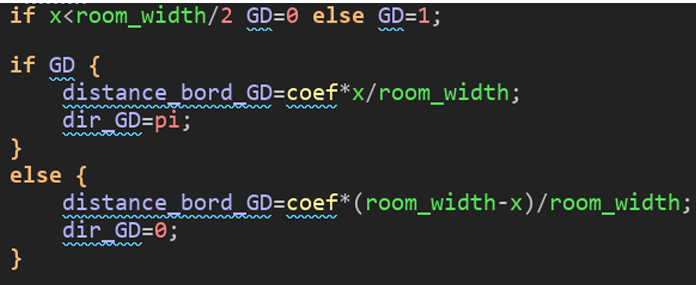
La première ligne vérifie si la créature se trouve à gauche de la pièce ou à droite. Selon le cas, dir_GD sera égale à 0 ou à pi (ce qui correspond à une orientation vers la gauche, ou vers la droite, dans GameMaker). quant à distance_bord_GD, le calcul proposé rend sa valeur (toujours positive) d'autant plus grande que la créature est proche du bord concerné (la formule rédigée en hâte lors de la JAM n'est pas parfaite, il aurait été plus logique qu'elle tienne compte de l'écart entre x et le centre de la pièce : room_width*0.5).
Maintenant que nous savons que dir_GD indique bien la gauche pour une créature à droite de l'écran, et la droite pour une créature à gauche de l'écran, et que nous savons également que distance_bord_GD aura une valeur d'autant plus grande que la créature sera près du bord, relisons notre code précédent :

Nous pouvons désormais comprendre que quelque soit la direction_aleatoire fixée pour la créature, la créature sera également soumise à un déplacement dans la direction indiquée par dir_GD, et que cette influence sera forte lorsque la créature sera près du bord de l'écran. Voilà comment la ramener vers le centre uniquement lorsqu'elle s'en éloigne !
Quant à cette étrange division par (1+distance_bord_GD), c'est une sorte de "normalisation" (pas tout à fait). En effet, il y aurait un problème si une créature tout à gauche de l'écran (par exemple), prenait pour direction_aleatoire la droite... en plus de sa marche aléatoire vers la droite, elle serait poussée encore plus vite vers la droite par distance_bord_GD*cos(dir_GD), et elle irait donc beaucoup trop vite ! Au final, en divisant par (1+distance_bord_GD), ce que nous faisons, c'est que nous "gommons" en quelque sorte la "marche aléatoire" lorsque la créature est très au bord, pour que seule la "marche forcée" s'exprime.
A noter que cette marche forcée sur les x (marche forcée horizontale) n'a aucun impact sur les y (marche verticale, soumise à des calculs similaires), permettant donc aux créatures de s'extraire des bords en diagonale par exemple, au gré du hasard !
Bon, mais... et le résultat alors ?
Quoi de mieux pour se faire une idée du résultat que de télécharger le jeu ? Il est gratuit ! Lancez des parties, éclatez-vous !
David (Maokoor)
P.S. : je vous ai dit que j'étais prof de maths dans une vie antérieure ? ^^
Files
Get MEURTRES EN COUPS LISSES
MEURTRES EN COUPS LISSES
Cute and funny Battle Royale !
| Status | In development |
| Authors | David FRANCOIS / Maokoor, Superneko3, ShrekSinj |
| Genre | Action |
| Tags | Animals, battleroyale, Cute, Funny, Local multiplayer |

Leave a comment
Log in with itch.io to leave a comment.